Pseudo-ring
In abstract algebra, a rng (also called a pseudo-ring or non-unital ring) is an algebraic structure satisfying the same properties as a ring, except that multiplication need not have an identity element. The term "rng" (pronounced rung) is meant to suggest that it is a "ring" without an "identity element", i.
Many authors do not require rings to have a multiplicative identity,[1] so the concept discussed here is just what these authors call a ring.
Contents |
Formal definition
Formally, a rng is a set R with two binary operations (+, ·) called addition and multiplication such that
- (R, +) is an abelian group,
- (R, ·) is a semigroup,
- Multiplication distributes over addition.
Homomorphisms between rngs are defined just like ring homomorphisms except that the requirement f(1) = 1 is dropped. That is, a rng homomorphism is a function f : R → S from one rng to another such that
- f(x + y) = f(x) + f(y)
- f(x·y) = f(x)·f(y)
for all x and y in R.
One can prove, however, that if a rng homomorphism f : R → S takes 1 to a unit s of S, then s = 1, or further that any rng homomorphism mapping any nonzero element to an element that is not a zero divisor in fact maps 1 to 1. Corollary : if a rng homomorphism maps a unit to a unit then it maps the identity of R to the identity of S.
Examples
Of course all rings are rngs. A simple example of a rng that is not a ring is given by the even integers with the ordinary addition and multiplication of integers. Another example is given by the set of all 3-by-3 real matrices whose bottom row is zero. Both of these examples are instances of the general fact that every (one- or two-sided) ideal is a rng.
Any abelian group can be made into a rng by taking the multiplication operation to be trivial (i.e. r·s = 0 for all r and s): such rng is called a zero ring. This rng will not have an identity unless it is trivial.
Rngs often appear naturally in functional analysis when linear operators on infinite-dimensional vector spaces are considered. Take for instance any infinite-dimensional vector space V and consider the set of all linear operators f : V → V with finite rank (i.e. dim f(V) < ∞). Together with addition and composition of operators, this is a rng, but not a ring. Another example is the rng of all real sequences that converge to 0, with component-wise operations.
Also, many test function spaces occurring in the theory of distributions consist of functions decreasing to zero at infinity, like e.g. Schwartz space. Thus, the function everywhere equal to one, which would be the only possible identity element for pointwise multiplication, cannot exist in such spaces, which therefore are rngs (for pointwise addition and multiplication). In particular, the real-valued continuous functions with compact support defined on some topological space, together with pointwise addition and multiplication, form a rng; this is not a ring unless the underlying space is compact.
Properties
Ideals and quotient rings can be defined for rngs in the same manner as for rings. The ideal theory of rngs is complicated by the fact that a rng, unlike a ring, need not contain any maximal ideals. Many theorems of ring theory are false for rngs.
Adjoining an identity element
Every rng R can be turned into a ring R^ by adjoining an identity element. The most general way in which to do this is to formally add an identity element 1 and let R^ consist of integral linear combinations of 1 and elements of R. That is, elements of R^ are of the form
- n·1 + r
where n is an integer and r ∈ R. Multiplication is defined by linearity:
- (n1 + r1)·(n2 + r2) = n1n2 + n1r2 + n2r1 + r1r2.
More formally, we can take R^ to be the cartesian product Z × R and define addition and multiplication by
- (n1, r1) + (n2, r2) = (n1 + n2, r1 + r2),
- (n1, r1)·(n2, r2) = (n1n2, n1r2 + n2r1 + r1r2).
The multiplicative identity of R^ is then (1, 0). There is a natural rng homomorphism j : R → R^ defined by j(r) = (0, r). This map has the following universal property:
- Given any ring S and any rng homomorphism f : R → S, there exists a unique ring homomorphisms g : R^ → S such that f = gj.
The map g can be defined by g(n, r) = n·1S + f(r). In a sense then, R^ is "the most general" ring containing R.
There is a natural surjective ring homomorphism R^ → Z which sends (n, r) to n. The kernel of this homomorphism is the image of R in R^. Since j is injective, we see that R is embedded as a (two-sided) ideal in R^ with the quotient ring R^/R isomorphic to Z. It follows that
- Every rng is an ideal in some ring, and every ideal of a ring is a rng.
Note that j is never surjective. So even when R already has an identity element the ring R^ will be a larger one with a different identity.
The process of adjoining an identity element to a rng can be formulated in the language of category theory. If we denote the category of all rings and ring homomorphisms by Ring and the category of all rngs and rng homomorphisms by Rng, then Ring is a (nonfull) subcategory of Rng. The construction of R^ given above yields a left adjoint to the inclusion functor I : Ring → Rng. This means that Ring is a reflective subcategory of Rng with reflector j : R → R^.
Properties weaker than having an identity
There are several properties that have been considered in the literature that are weaker than having an identity element, but not so general. For example:
- Rings with enough idempotents: A rng R is said to be a ring with enough idempotents in case there exists a subset E of R given by idempotents (i.e. e2 = e for all e in E) orthogonal (i.e. ef = 0 for all e≠f in E) such that
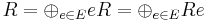 .
. - Rings with local units: A rng R is said to be a ring with local units in case for every finite set r1, r2, ..., rt in R we can find e in R such that e2 = e and eri = ri = rie for every i
- s-unital rings: A rng R is said to be s-unital in case for every finite set r1, r2, ..., rt in R we can find s in R such that sri = ri = ris for every i.
- Firm rings: A rng R is said to be firm if the canonical homomorphism
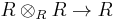 given by
given by 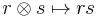 is an isomorphism.
is an isomorphism. - Idempotent rings: A rng R is said to be idempotent in case R2 = R, that is, for every element r of R we can find elements ri and si in R such that
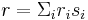
It is not hard to check that these properties are weaker than having an identity element and weaker than the previous one.
- Rings are rings with enough idempotents, using E = {1}. A ring with enough idempotents that has no identity is for example the ring of infinite matrices over a field with just a finite number of nonzero entries. The matrices that have just 1 over one element in the main diagonal and 0 otherwise are the orthogonal idempotents.
- Rings with enough idempotents are rings with local units just taking finite sums of the orthogonal idempotents to satisfy the definition.
- Rings with local units are in particular s-unital, s-unital rings are firm and firm rings are idempotent.
Zero rng
A rng (R, +, · ) is said to be a zero rng if the product of any two elements in R is the additive identity 0.
A zero rng that has a multiplicative identity (that is, which is a ring) must be the trivial rng. Therefore, the concept of a zero rng is interesting only for rngs that are not rings.
Any abelian group can be turned into a zero ring by letting a · b = 0 for every a, b in the group (and letting + be the group operation of that abelian group).
References
- ^ Dummit, David S.; Foote, Richard M. (July 14, 2003). Abstract Algebra 3E. Wiley. ISBN 978-0471433347., Herstein, I.N. (January 1, 1996). Abstract Algebra 3E. Wiley. ISBN 978-0471368793.